The K-Means Clustering Algorithm is one of the most straight-forward clustering algorithm in data science. It aims at solving Vector Quantization problems. Given a set of sample points and the number of clusters k, the algorithm starts from k initial centers points and goes on the following procedure:
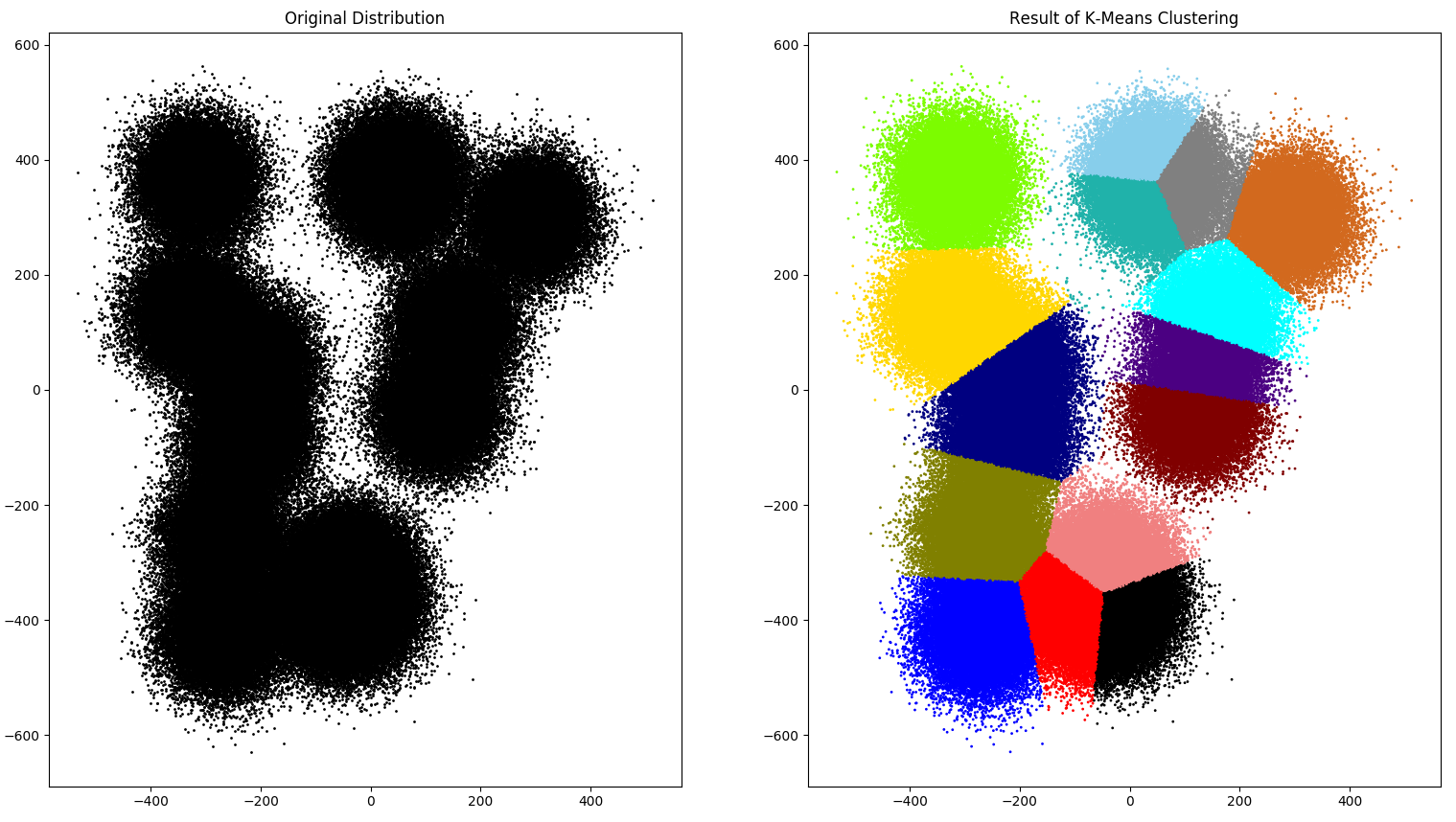
We will be dealing with K-Means on a 2-Dimensional data set. For example, the following is an example data set, with number of data sample points p = 450,000 and desired number of clusters (colors) c = 15:

K-means cannot always give an elegant solution, but it is very straightforward and easy to understand.
The input of your algorithm will be a txt file of the following format:
450000 / 15
181.32907969, 251.07429196, 0
-189.28197631, -360.18581742, 0
333.06486750, 194.89272514, 0
175.15397040, 257.92706689, 0
-184.17403621, -420.23277421, 0
...
...
-139.93631124, -308.79563496, 0
173.08555561, -154.49741085, 0
188.38953238, 312.91741170, 0
247.30736986, 190.62523729, 0
46.01590445, 225.99338366, 0
Explanation of the input file:
p / c separated by a slash, where p is the total number of sample points, and c is the desired number of clusters.
p lines in the form x, y, 0, each describing a data point's coordinate (x, y), and the original color id 0 (because they have not been clustered, so we consider they are all initially "black"). Both x and y are represented in a signed floating point number, each have 8 digits after the decimal point.
We have implemented a simple sequential solution in C++. You can download the framework from here.
make
./kmeans <input.txt> <result.txt>
make cleanYou should try your best to parallelize and optimize the given K-Means with any techniques you can come up with. Unlike Homework 5, in Project 3 here you can perform any shared-memory optimization techniques you wish, including but not limited to:
kmeans.cpp and kmeans.h, you are only allowed to add / modify things in the indicated area. (They have been clearly narrated in the comments. Read them carefully please.) Feel free to modify the Makefile and add flags that you need.
The initial center points will be picked randomly among the data points, but the random seed is fixed to 5201314 (as you can notice the line of code srand(5201314); in kmeans.cpp). This ensures that, on the same execution environment, with the same input dataset, we always pick the same set of initial center points. This property is very important for our testing. We will compare your output with the reference output, and see if the clusters match each other. The same cluster may get different color ids in reference solution and your output, but as long as it is a one-to-one mapping, it is accepted.
Like these two clustering results, they get different colors, but every point actually goes to the correct cluster:
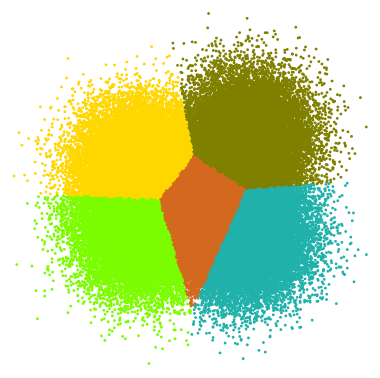
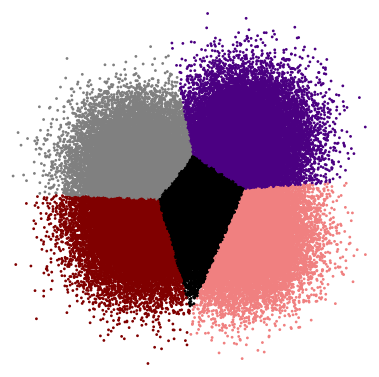 Accepted √
Accepted √
Your program will write the calculated clustering information into the specified output txt file. The content of the output file is similar to the input, except that the color information has been filled. For example:
450000 / 15
181.32907969, 251.07429196, 11
-189.28197631, -360.18581742, 6
333.06486750, 194.89272514, 7
175.15397040, 257.92706689, 11
-184.17403621, -420.23277421, 6
...
...
-139.93631124, -308.79563496, 6
173.08555561, -154.49741085, 9
188.38953238, 312.91741170, 13
247.30736986, 190.62523729, 4
46.01590445, 225.99338366, 8
Each color id represents a unique color (i.e. the cluster that the data point finally belongs to).
Meanwhile, your console will reveal the total time elapsed for the algorithm execution. Time is only ticked around the k-Means algorithm. I/O stuff is not included. So your optimization should exactly focus on the main body of the algorithm.
We provide two Python tools for you, generate.py and plot.py in the framework. Make sure you have a workable Python ≥ 3.5. Also, install these packages with pip3 if you do not have them yet:
scikit-learnnumpyscipymatplotlib
Use make gen FILE=<data-file.txt> to generate a data set. It will prompt the following things in the console, and wait for you to give the parameters. Simply hit Enter if you want the default option.
Enter dataset parameters:
* # of samples (100,000 ~ 800,000) [default = 450,000]:
* # of theoretical clusters (1 ~ 20) [default = 15]:
* |Range| where centers can be (100. ~ 800.) [default = 450.]:
* Standard deviation of a cluster (10. ~ 100.) [default = 50.]:
It will generate a bunch of clusters with randomly picked centers, and distribute the data points around them using Gaussian distribution. |Range| means the limit of absolute value of coordinate x and y for every sample, and Standard deviation determines how disperse the points will be.
Use make plot FILE=<result.txt> to plot the clustering result. It uses PyPlot to generate a plot in a pop-up window. With large number of data points, the plotting may be VERY slow. Please be patient.
We will be using git for this project as well. Refer to previous Git Usage Guide for basic git usage. Create your team's git repo for Project 3 on GitHub, initialize your framework directory as a git repository (which means it directly contains kmeans.cpp ...), and push your work onto your remote repository.
Submit your work to Autolab with an archive project3.tar, which is created through:
git clone --bare YOUR-TEAM-REPO-URL.git .git
tar czvf project3.tar .git
You can add your own code files, as long as they fit in the project, and you have wrote the correct Makefile for integrating them.
Due to the poor performance of Autolab server (服 xiǎo 务 shuǐ 器 guǎn), we will only autograde your submission on 100,000 ~ 200,000 sized data sets and give you a score according to correctness. The execution time on Autolab will also be given, but that is only a reference.
Step 1: If you submitted the correct algorithm onto Autolab, meanwhile it makes meaningful uses of multithreading, you get 60% of the total score. (Memory leak check with valgrind is also included)
Step 2: After the autograding deadline, we will run your algorithms on a much stronger and stabler server. We will run it on a huuuuuge data set (450,000 ~ 800,000 points) for several times, and take the average execution time tavg. If you have earned the 60%, the rest 40% will be given based on the performance of your algorithm on the strong server. Fastest 15 groups get full 40%, top 16~35 get 30%, top 36~55 get 20%, and the rest get 10%. NOTE: If your program crashes on this huge data set, you will get zero for this phase.
No hints for this project! @v@; I believe you can think of really great ideas for optimizing this classic algorithm. Just a reference: If you really did some work properly, you should at least achieve 3x speedup with 4 threads.
If you came up with a really incredible optimization approach which is accurate and highly parallelizable, please come to TAs. We warmly welcome your sparkling ideas and may consider giving you a bonus.
Autolab Server (Just for your reference. Tune your performance to the Star Lab Server):